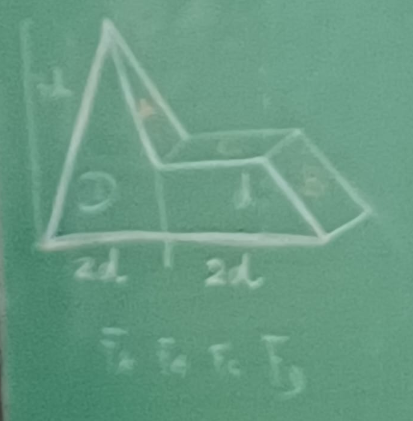I’ve 3D modeled the weird shape my physics 2 teacher made on her class.

The project files (the OpenSCAD ‘code’) are available on my GitHub.

Rendered preview of the shape in OpenSCAD, it's a pyramid with a trapezoid-like shape glued to its right

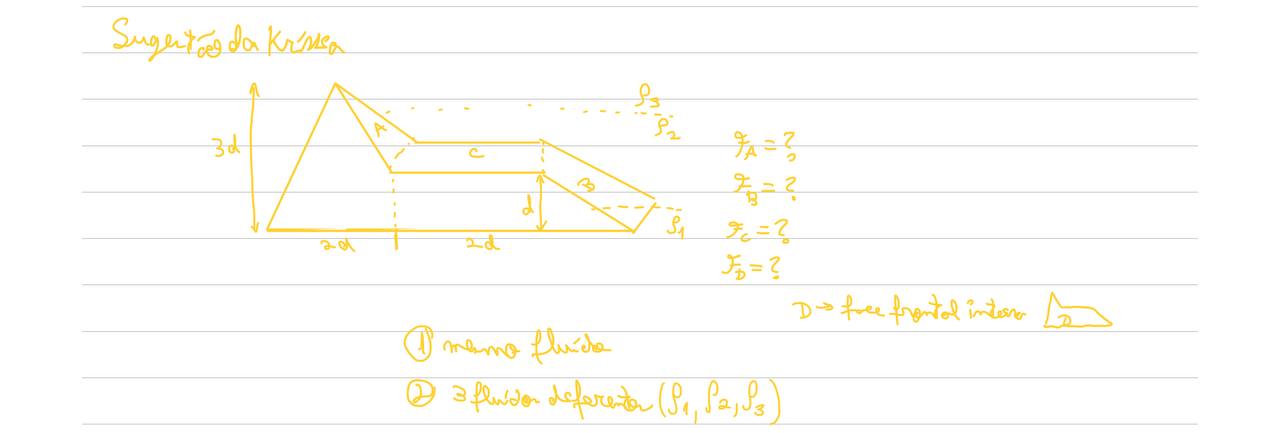
The Exercise

She drew this shape on the board as a training exercise suggestion for the liquid stuff part of the subject, so I offered to 3D print it for her.

Screenshot of the exercise in my tablet, a drawing of the shape is shown and the exercise is handwritten around it. It asks for the pressure in 4 of the faces, named A, B, C and D, if you had a container of that shape filled with liquid. Then, part two asks for the same thing but if you had 3 different liquids with different densities filling the container.

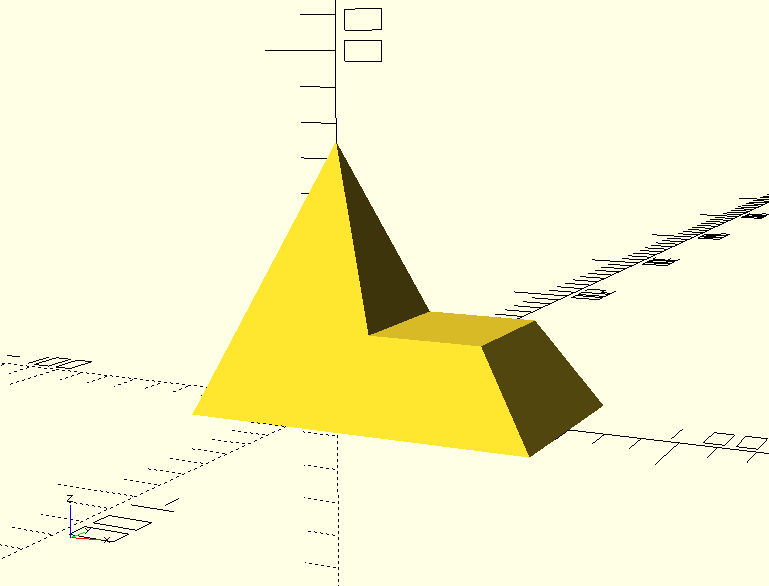
Modeling the Shape

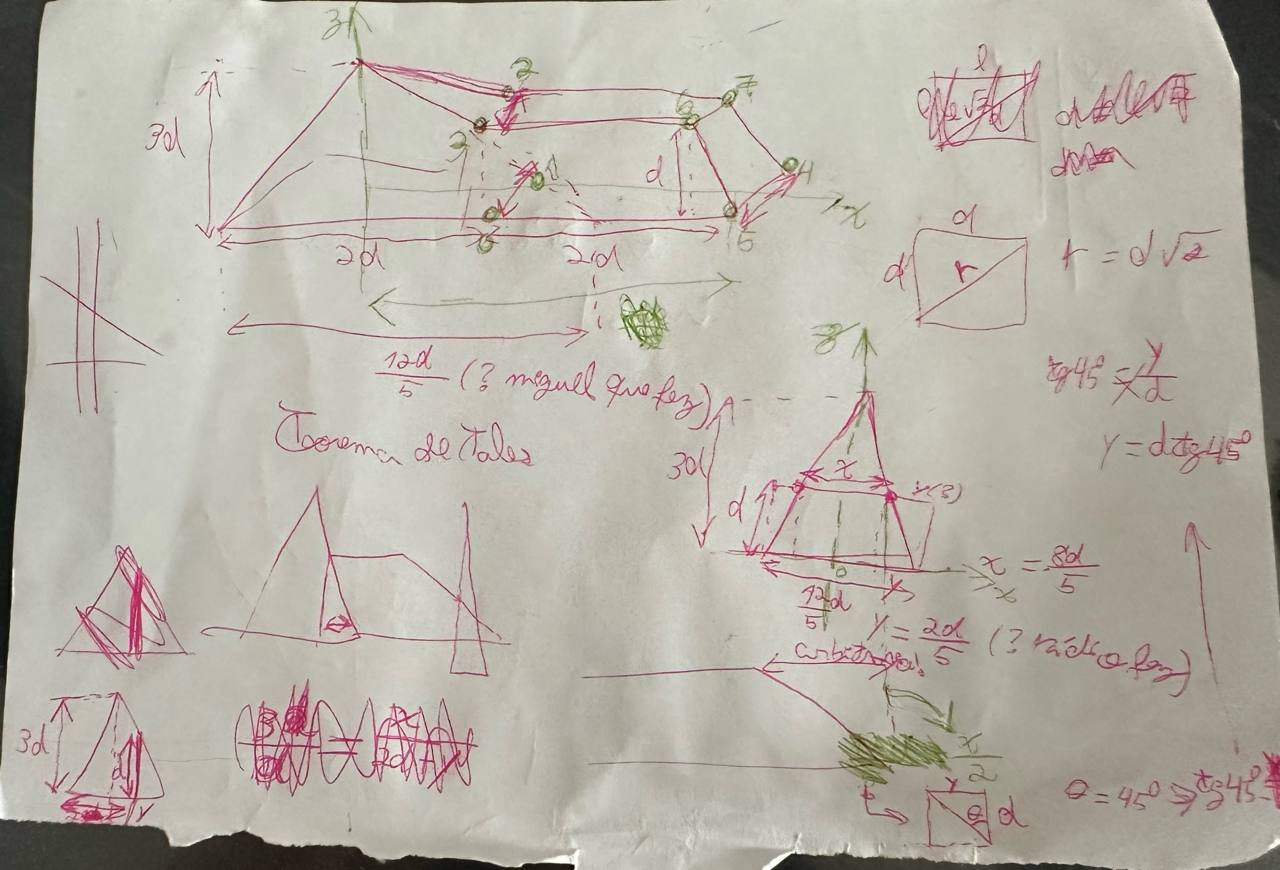
In order to model this in 3D and then 3D print it, first I had to calculate the length of the side of the pyramid’s square base. I had the Thales Theorem waay back from high school in mind.

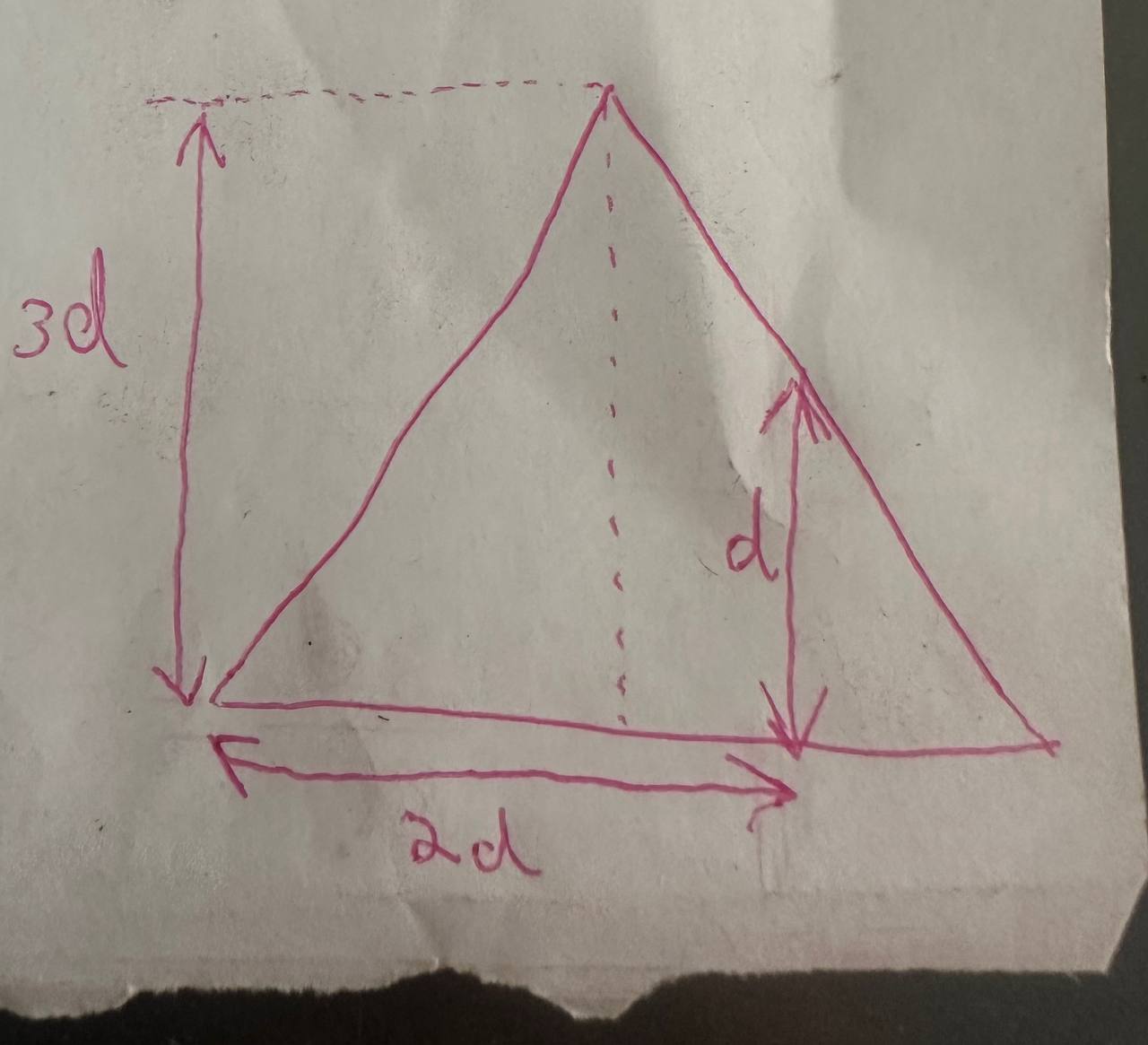
thales theorem drawing of a triangle

However, it’s been a while since I’ve last messed with trigonometry so it didn’t really work out. Therefore, I asked for help at the GELOS off-topic channel, because I know some of my friends there are good in math stuff.

So Miguel calculated that length as (12/5)*d (line 4):

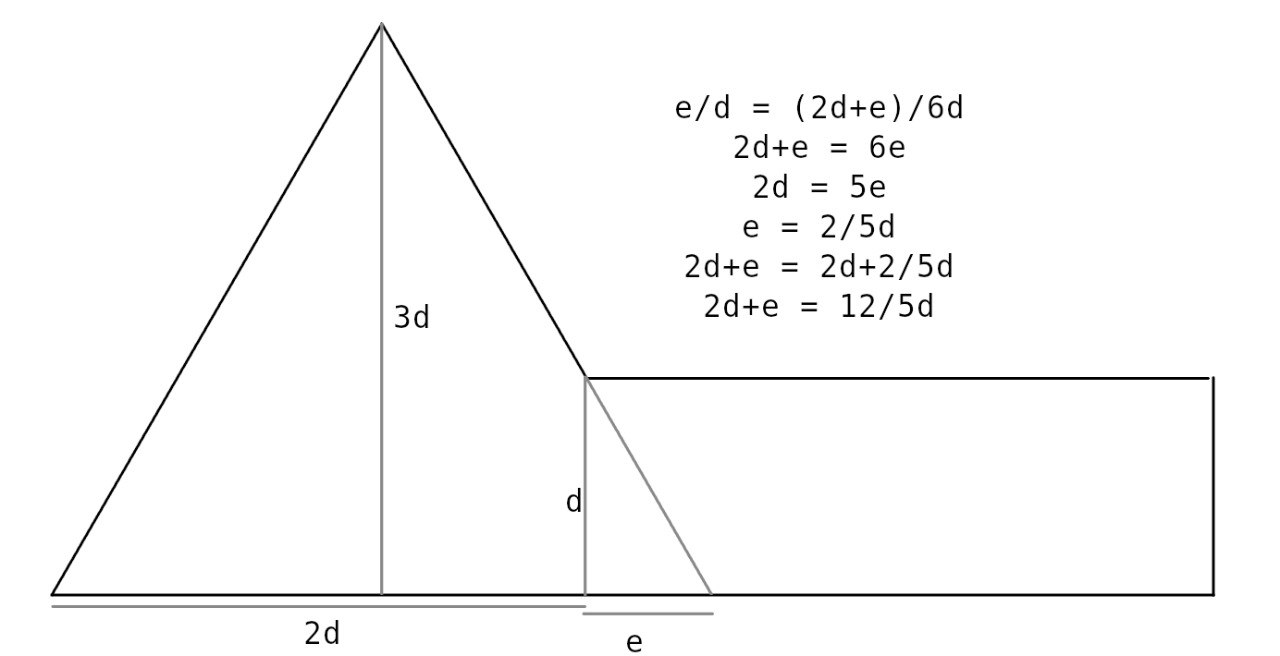
Thales theorem calculation of the aforementioned size

For the coordinates of the top vertices of the trapezoid, since the pyramid gets thinner at the top (because, well, it’s a pyramid), I once again asked for help and Rádio from GELOS calculated it (line 17):

Calculating the relative positions of the vertices of the trapezoid at height d related to the pyramid

So now it was up to me to model the shape!

I chose d = 100/4 mm, because I wanted the final shape to have a length (4d) of 10 cm (for the unitedstadians reading this, this appears to be around the size of two golf tees laid end‑to‑end). While building the shape, however, I was very careful to avoid hardcoding any values. This means you can simply change the d constant value (line 3) and everything will scale correctly!

When I was almost done, I noticed the inclination of the right end of the trapezoid could be arbitrarily chosen so I chose 55 degrees bc it looked good (line 20). So, on the below image, θ = 55deg and t = d * tan(90-θ) = 0.7*d.

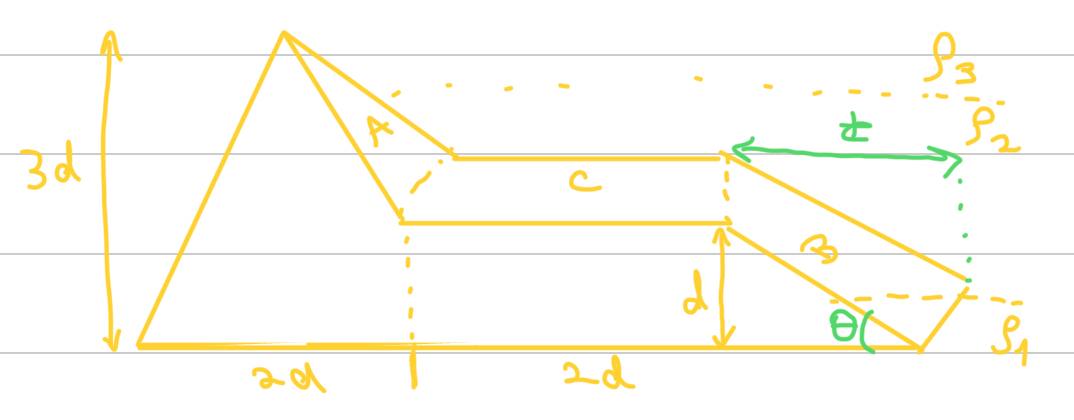
Image of the shape in my tablet again, now shoing an angle theta for the right wall of the shape

Just as with d, changing the iatr variable will accordingly change the shape to the correct angle with no extra steps.

So, after an afternoon of OpenSCADing, the shape is done!

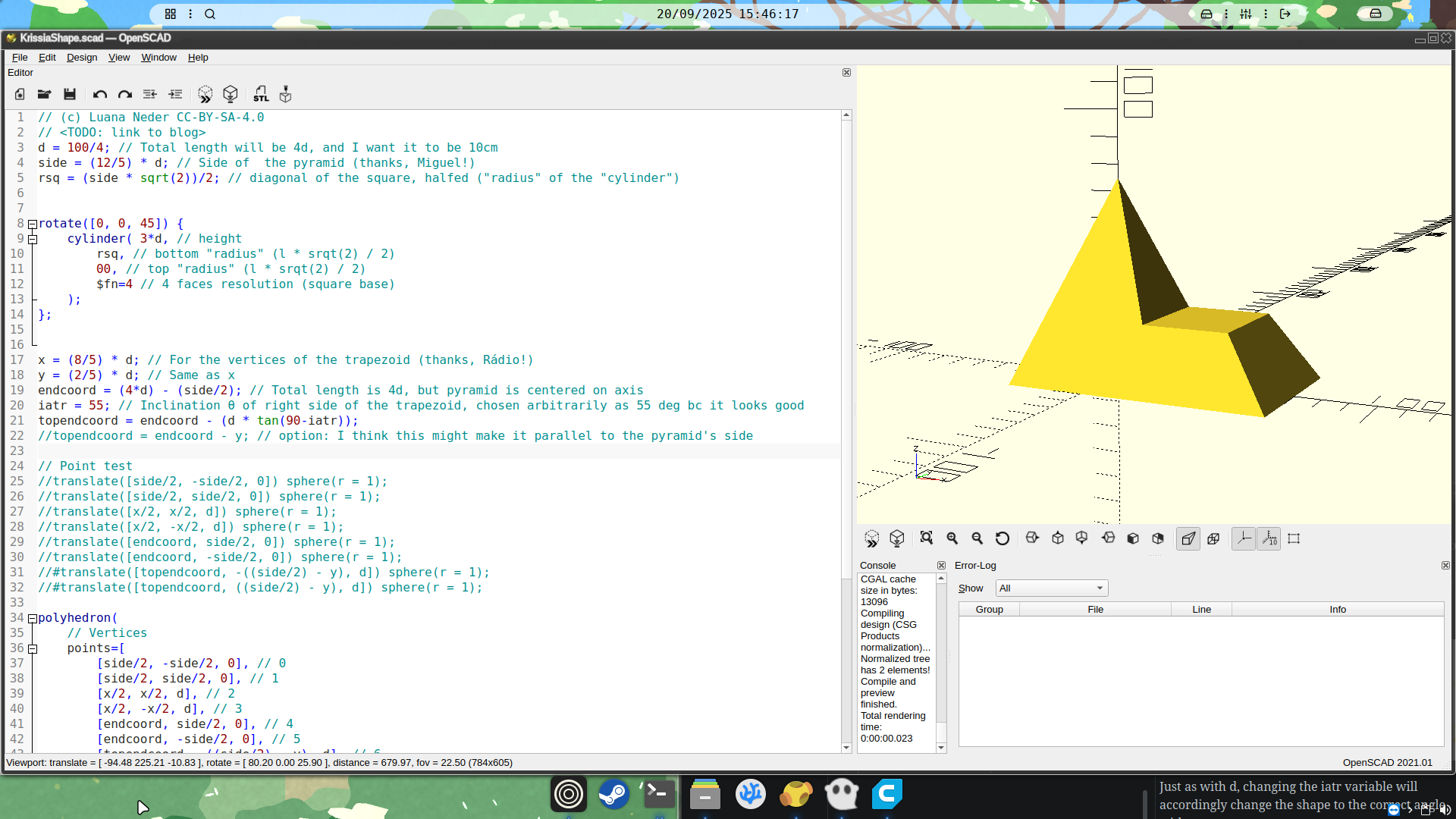
OpenSCAD screenshot showing the final shape and the full OpenSCAD window

Final Result

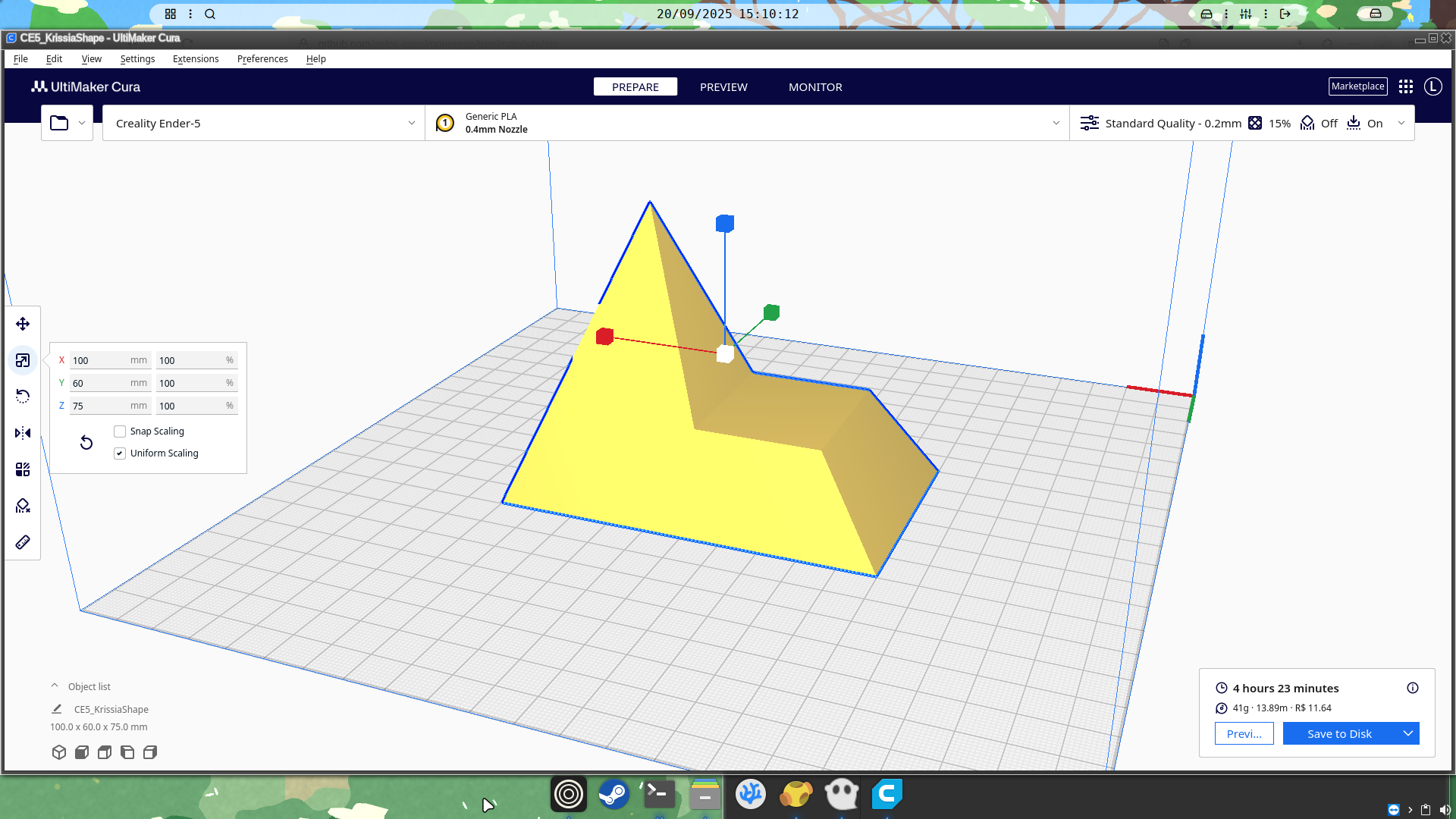
Exporting and loading the STL on Cura, we can see it’s indeed on our expected size. This means Miguel’s and Rádio’s calculations are indeed correct, and The Shape is ready to be printed!

Screenshot of Cura with the sliced shape, measuring exactly 100mm in length, 75mm in height and 60mm of depth

After some hours, here’s our final result!

Photo of the ready shape, 3D printed in fluorescent blue PLA, still attached to the 3D printer

Photo of the ready shape, 3D printed in fluorescent blue PLA

(as you can see, yes I had some adhesion problems and added a Cura raft to get better contact surface)

You can download the stl here.

Welp, it’s Expedition 33 time now!

Thanks for reading, and let’s hope no shapes as weird as this one show up on the tests!

Extra

Here’s the original drawing on the board and my drafts on paper while making this (lots of wrong stuff there probably, maybe just ignore it lol)

the shape drawn on a blackboard

a piece of paper full of random drawings and calculations